這次提到的概念是比上次的「 Symmetric Cryptography 」來的更進階的「 Asymmetric Cryptography (非對稱加密) 」,其概念被廣泛運用在數位簽章。
前言#
若你還不了解「 Symmetric Cryptography (對稱加密) 」是什麼,建議在閱讀本文前,先看看我前一篇文章「對稱加密 (Symmetric Cryptography)」,否則可能會搞不清楚在本篇中,基於上一篇介紹裡所使用的單字意思。
對稱加密所無法解決的難題#
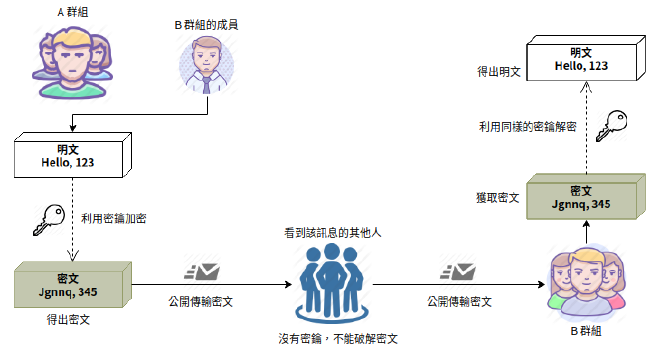
在上一篇的對稱加密概念介紹中,其作法可以有效的使多方溝通之間存在更高的安全性,但共享密鑰也同時意味著「 對方有與你相同的權限 」,你能加密訊息後發布,對方也能,你能透過密鑰解密,對方也能。
在很多時候,A 方與 B 方雖然需要加密溝通,但卻必須分清楚雙方身份,否則可能存在偽造的風險,注意,這邊所說的 A、B 方並不一定是單一的,他可以是群體,也就是說有某一群人稱為A,某另一群人稱為B,而雙方都有著相同的密鑰可以用來加密及解密訊息,這兩群人透過對稱加密來加密訊息並溝通,但這僅能保護雙方在溝通時,不被非 A、B 兩方的人了解密文意思而已,並不能驗證該訊息的發送者身份是 A 還是 B,因為雙方的密鑰是相同的,因此萬一有某人為 B 方,而他卻聲稱自己是 A 方的人,並且使用密鑰加密訊息發給 B 方,那 B 方又該如何驗證該人的身份?
Asymmetric Cryptography (非對稱加密)#
為了解決上述問題,我們必須改成「 加密與解密使用不同密鑰 」,於是「 Asymmetric Cryptography (非對稱加密) 」誕生了。
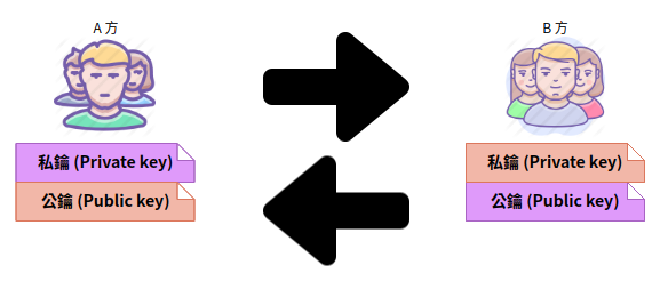
- 公鑰、私鑰
- 由於加密與解密需要使用不同密鑰,因此雙方在溝通前可以各別生產一對密鑰,這一對密鑰一把當公鑰,一把當私鑰,注意,這兩把密鑰它們之間有著數學關連,至於分成公、私鑰是做什麼的,等等會解釋,目前只要先記得,這兩把鑰匙是一對的。
- 在這邊提醒一個重點,雖然說一對公鑰與私鑰之間有著關聯,可是並不能透過公鑰推算出對應的私鑰,也就是說,今天就算別人知道你的公鑰,對方也是幾乎無法破解出你的私鑰。(有些算法當中,其
公鑰是私鑰推算出的)

- 釋出公鑰
將公鑰交給對方,用於給對方在之後進行解密使用。
- 加密、解密
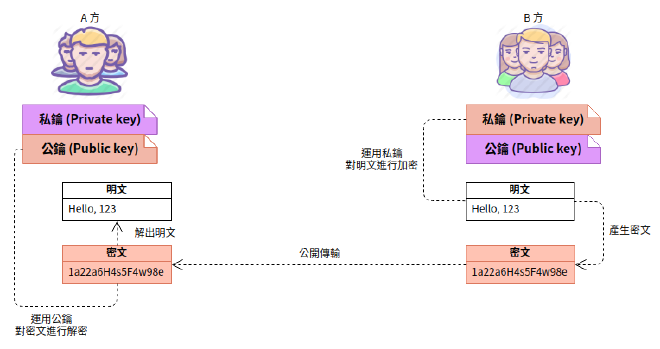
- 接下來就是非對稱加密的特殊之處了,這時候雙方手上都持有自己的私鑰及對方的公鑰,「 自己的私鑰 」用於「 加密 」,「 對方的公鑰 」用於「 解密 」。
- 下方示意圖是B 方傳送訊息給A 方的情境,B 方運用自己的私鑰加密後傳送給A 方,而A 方則使用B 方的公鑰進行解密。
- 運用私鑰所加密的訊息只有該私鑰所對應的公鑰才能解密。
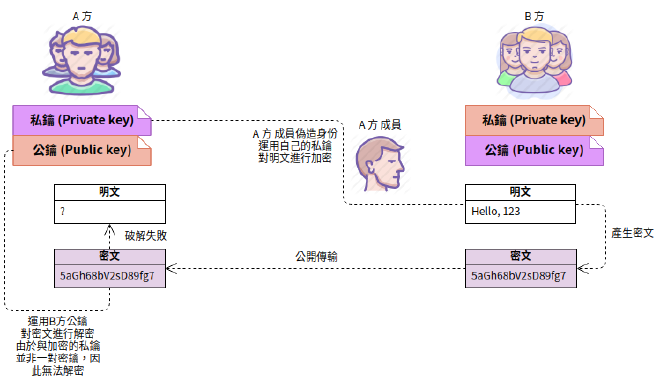
加密解密 - 所以萬一有人想偽造身份,除非是偷到私鑰,否則是不可行的。
運用#
非對稱加密被運用在許多地方,而常見的 數位簽章 (Digital Signature) 也是利用此概念來達到辨識身份及加密的原理。另外,許多標榜像是加密傳輸、加密聊天等應用,也都看得到非對稱加密的蹤影,只要私鑰不洩漏,基本上不會有第二則密文可以被該公鑰解密成有意義的明文。
P.S. 非對稱加密中常見的加密演算法有:
RSA、DH、ECDH、ECDSA (橢圓曲線數字簽名算法)、ElGamal、SM2。
有興趣的朋友可以點擊連結或自行上網研究。