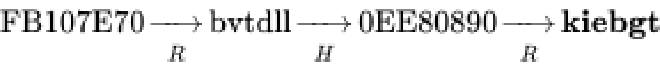Encode、Encrypt and Hash are different！

Cryptography - 本文屬於一個選集。

§ : 本文

Encode (編碼)、Encrypt (加密)、Hash (雜湊) 一直令許多新手們搞混，雖然說可能運算後的結果看起來都是一串亂碼，但原理及使用場合卻天差地遠，千萬不要再分不清處了！

Encode (編碼)
#

在計算機中，需要儲存大量資料，而這些資料基於各國的語言不同，可能是基本的英文或是博大精深的中文，中文又分簡體、繁體，甚至是由右至左書寫的阿拉伯文等。

雖然各種國家的文字零零種種非常多，尤其中文數量更是大的驚人，但這些文字對計算機來說都只是「字元」，更精確來說都只是機器語言，也就是常聽見的「0、1」，所以儲存上並難不倒它，問題就出在，如何在存放與顯示之間做格式的轉換？

ASCII
#
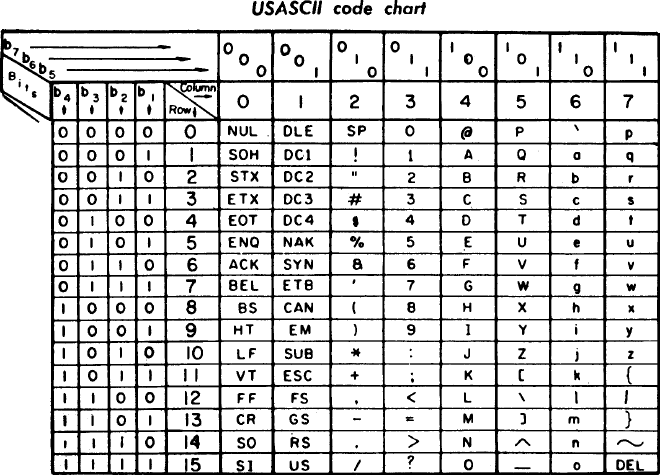
舉例剛開始美國人使用的編碼「ASCII」，全名「American Standard Code for Information Interchange (美國資訊交換標準代碼)」，主要是用來顯示基本的 阿拉伯數字、26 個英文字母(大小寫)、英式標點符號。但這很快就使得在其他語系的國家顯示上出現問題，例如西歐語言就無法套用在 ASCII 上。
1968年版ASCII編碼速見表｜圖源自 Wiki 維基百科
雖然後來也使用 EASCII 解決了部分西歐語言的顯示問題，但還是有著各式各樣的語言在顯示上有問題，這也是導致為什麼會有那麼多種編碼的原因之一，儘管有著這麼多的編碼，但也出現了一個新的問題「如何統一」？直到「Unicode」被發明。

Unicode (UTF)
#
「Unicode」簡稱「UTF」又稱「萬國碼、統一碼」，是一種被大家公認的標準編碼。
它最大的優點在於，該編碼納入了世界上大部分的文字系統，也就是將那些雜亂的編碼給統整了，所以其實它是一種「編碼集」，這也就使得計算機能夠更簡單方便的呈現和處理文字。

說了這麼多，你可能已經發現，名詞「Encode (編碼)」其實就只是在指資料的格式，放在動詞上解釋就只是轉換資料格式的過程。因此，編碼僅僅只是將文字轉換成不同格式做儲存、顯示等，並無實質上的加密作用。

Decode(解碼)
#

基本上就是將 Encode(編碼) 過後的資料做反向編碼的動作。
其實從字面上意思也不難理解「編」與「解」所表達的含意，就像是加工與還原般。

Encrypt (加密)
#

基於資料的隱私及安全性考量，在許多時候我們不得將資料給加密以確保資料內容不被輕易讀取。
但要特別在此聲明的一點是，這裡所指的「Encrypt (加密)」並非是大家常使用的「帳號、密碼」系統。
以往我們不希望他人讀取自己較私人的訊息時，我們會在這些資料被讀取前請求驗證身份，舉例將檔案放在保險箱中，若是密碼不正確則無法開啟保險箱，藉此達到資料不被讀取的安全功能。
理論上沒問題，但這其實有個致命的缺點… 如果鎖被破壞呢？

萬一有些方法能破壞這些鎖，進而達到不用輸入密碼也能存取的動作，那這種加密豈不是失去作用了。

會導致這樣的原因主要是因為，這些聲稱加密的檔案其實並沒有被真正的「加密運算」，只是在外層加上了一道防護而已。而安全的加密應該是連同裡面的資料進行改變，這麼一來若是無法有相對應的金鑰，則無法解密資料。

可以想像成 Encrypt (加密) 就是將 Encode (編碼) 中融入了 Key (密鑰) 及 Algorithm (演算法) 的元素，使 Key (密鑰) 參與了這整個利用 Algorithm (演算法) 轉換格式的過程，因此若是缺少 Key (密鑰) 是無法反推算原始含意的。

而加密的方式有成千上萬中種，大致上可以分成兩類，分別是「Symmetric-key algorithm (對稱加密)」及「Asymmetric Cryptography (非對稱加密)」。
對這部份想更深入了解的朋友可以看看我之前寫的文章「」及「」。

Decrypt (解密)
#

指對於「Encrypt (加密)」過的檔案使用對應的 Key(密鑰) 進行反運算以得出原本內容的過程。

Hash (雜湊)
#

相較於上述的 Encode (編碼) 及 Encrypt (加密) 來說，Hash (雜湊) 算是個特別的存在。
直接道出重點的話就是「Hash (雜湊) 是不可逆的」。

可逆性 (Reversibility)
#
顧名思義就是可以逆向回朔原始狀態的意思。與其相反的詞為「不可逆性 (Irreversibility)」。
好比上述的「Encode (編碼)」，基本上各式各樣的編碼方式及編碼對應表在網絡上都可以搜尋的到，也就表示任何人都可以對這些編碼進行解碼的動作，因為方法是公開的。(當然，自創的編碼例外)
再者，「Encrypt (加密)」也可以被持有「Key (密鑰)」者透過「Decrypt (解密)」的動作還原出原始的含意。
這些可以被成功回朔至原始含意的都代表含有 可逆性 (Reversibility)。

不可逆性 (Irreversibility)
#
與上述的可逆性 (Reversibility)擁有相反性質，表示無法單純透過字串或亂碼追朔其原始含意。
Hash (雜湊) 就是這樣的存在。

那麼是如何做到 不可逆性 (Irreversibility) 的呢？

破壞性的運算
#
有著可逆性 (Reversibility)的主要原因是因為其內容依舊被「完整的保留」，只是換了種儲存方式而已。但Hash (雜湊)則不會如此，也就是說 Hash (雜湊) 會將原始的資料給破壞保存。

舉個例子，我們都知道的除法。
除法「16 / 8」會等於「2」，若試問你「X / 8」結果為「2」，你依然能透過「2 * 8」得出「X = 16」，因為「除法」可以被理解成是「乘法的反運算」。
這個道理大家都懂，那麼若是取餘數呢？(或說是取模數)
舉例「16 Mod 4」會是「0」，因為 16 能被 4 整除。
而「16 Mod 5」則會是「1」，問題來了，若試問你「X Mod 5」結果為「1」，你能推出「X」的值嗎？
這可能的值將有無限多種，你無法光靠保留下來的資訊推算原始內容，因此就可以達到 不可逆性 (Irreversibility) 的效果。

這只是其中一個簡單的例子，而 Hash (雜湊) 中含有各種類似的概念以確保運算後的結果不能被反推。
並且 Hash (雜湊) 有著特點，就是當輸入的內容相差了哪怕只有一點，也會導致雜湊結果截然不同。

舉例「alpaca blog」的 SHA-256 雜湊為「58e93956c3cc49342b607a931e4fd60e37518d7f21f29e1dfc968d4be98c976a」。那在後面加個小點變成「alpaca blog.」的 SHA-256 會是長怎樣呢？
答案是「3e445a9b450005d71ce28992d24871ddd5bcf5495a6eb52d3fe91f594cf3c35d」。
完全不同的結果，若要分析破解雜湊值根本無跡可尋。

但也因此，其實雜湊是「可能會重複」的！
畢竟即使擁有「2^256+1」種可能性的 SHA-256 也不能裝下第「2^256+2」種輸入還不產出重複的輸出結果吧！
只是很難找到重複的兩筆資料，因為實在是太多種可能性了！
即使找到了，但也很難是有意義的資料，通常是亂碼，這也可以使人為修改幾乎成為不可能的事情。

(ps. 許多雜湊是不論輸入的字串長度多長，輸出的長度皆相同的。舉例「SHA-256」就是輸出 256 bits，大小寫英文及數字，字元長度為「64」，而 MD5 則固定輸出 128 bits，大小寫英文及數字，字元長度為「32」。)

大致上都了解雜湊的特性了
那麼問題來了，什麼情況下我們會需要將資料 Hash (雜湊) ？
既然不能被還原，那要那串雜湊過後的亂碼有什麼用？

驗證資料完整性
#

由於基本上很難找到兩筆有意義的重複雜湊值，因此就可以透過此方式來驗證檔案的完整性。

舉例「虛擬貨幣」就使用這點來驗證每筆交易的可信度，又或者你可能在下載某些檔案時，就曾看過官方在該檔案旁標示的「識別亂碼」，就是使用雜湊的原理。
常見的雜湊就有「SHA-1、SHA-256、MD5」等。

每個在計算機上的「File (檔案)」不論是 mp3、mp4、txt、jpg、png、gif 等，對電腦來說都只是一串很長的文字，更精確來說都只是 0 與 1。
既然如此，那麼我們就可以將檔案進行雜湊運算！

有什麼用處？

試想一下，是否曾經聽過駭客入侵網站後，將原有的檔案竄改加入病毒使他人下載並執行到被加工檔案的事件。若是有個機制能檢測檔案是否遭到竄改，但過程又不必要去比對整個檔案的內容(太耗效能資源)，該怎麼做？
看看上面的 Hash (雜湊) 特性，就不難理解它可以有效的做到這點。

官方在釋出檔案的同時，附上一段該檔案的雜湊值及雜湊演算法，使用者下載了該檔案後，可以自己將檔案再次經過雜湊後比對是否跟官方所附上的雜湊值一致，若不一致表示該檔案被竄改過！

例如 bitcoin.org 網站提供大家下載「bitcoin core」比特幣錢包。
並且付上了對於檔案的數字簽名。
內容大致上長這樣：

-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA256

43416854330914992bbba2d0e9adf2a6fff4130be9af8ae2ef1186e743d9a3fe  bitcoin-0.21.0-aarch64-linux-gnu.tar.gz
f028af308eda45a3c4c90f9332f96b075bf21e3495c945ebce48597151808176  bitcoin-0.21.0-arm-linux-gnueabihf.tar.gz
695fb624fa6423f5da4f443b60763dd1d77488bfe5ef63760904a7b54e91298d  bitcoin-0.21.0-osx64.tar.gz
6223fd23d07133a6bfa2aa3d2554a09dc1d790d28ce67b0085d3fdcc1c126e05  bitcoin-0.21.0-osx.dmg
f8b2adfeae021a672effbc7bd40d5c48d6b94e53b2dd660f787340bf1a52e4e9  bitcoin-0.21.0-riscv64-linux-gnu.tar.gz
1a91202c62ee49fb64d57a52b8d6d01cd392fffcbef257b573800f9289655f37  bitcoin-0.21.0.tar.gz
54050748ef4d4f000ea1ece472491b3e5fd546efc74ed52119354b2893f6624b  bitcoin-0.21.0-win64-setup.exe
1d0052c4ce80227fb6d0bc1c4e673ba21033e219c1f935d25f130ef7f43360d4  bitcoin-0.21.0-win64.zip
da7766775e3f9c98d7a9145429f2be8297c2672fe5b118fd3dc2411fb48e0032  bitcoin-0.21.0-x86_64-linux-gnu.tar.gz
-----BEGIN PGP SIGNATURE-----
Version: GnuPG v1.4.11 (GNU/Linux)

iQIcBAEBCAAGBQJgADqTAAoJEJDIAZ42wulkjtkQAJwlSTDinKsxZIMky3MeVhwB
CmxxYiMLPQA8bwgxyc4RaTxUrqL2oExPOtfcDzcR1WbQe12niG40N/2yrtf66lG9
KbSsQD6nKat9B3mCk9/jNkJHWmq5JJbOyfRs2mex75Lj7UHaPPrqh2rMfEewljed
kHkDuaqeqYlTAh981WqLD+l5jnpQZqBSrcz3YTTvXWd7xKfFSVzqF/tD4CQFrPX2
9b2BLzA/u+29Z3s+zio1l5c7fikNDd404T5U/y+NMOyCmgT4eiDGLQPlEpoGNq3w
GYU7FNZUO9xXeatx4PI8qiq5mIK46UwfPUTeruTzNrHsME7YioUa87uSYKM8jqwP
FSnbhYoUqCB/wPaKZwEF+2WzG88yj2+PzalVt8cnjRnTQ77COtHJqs8AjLWnVACF
LluplM16xyiLn0FWkrEHyi5HlI+X+cqIiTtehojMBXIkHugIYMnT5XB9llh5OWXg
Bp1UGupojLXYuMNF5R6cU5Iq+xJjbUiQ/PDm38MBlFlQ9RzRCYyZpMYZE3K9p789
jpjdYdMPtzkYlIKD87S89JtE1s6i/SkTPhebyu/328rqkqnNKSCHnuB7Fy2iEKJj
5kLs/LjY8yxSMuGeNl6LhWGKVZKy0AS/BztSHr2jgThfhN1BemFRcViSvcXhMeNw
ka8Z9KLt/N0ziabBexAw
=bi4p
-----END PGP SIGNATURE-----

在第二行的位置，官方標示了「Hash 方式為 SHA256」，接著就列出了各個檔案的雜湊值供大家驗證，可是該文檔也是可能受到偽造的，那怎麼辦？
還記得前面所說的「非對稱加密」嗎？在此情境當中被用在了「數字簽名」，並且將簽章寫在文檔最後，也就是最後那串很長的亂碼。

官方將前面的整段「BEGIN PGP SIGNED MESSAGE 與 -----BEGIN PGP SIGNATURE----- 中間」的內容給簽章成「-----BEGIN PGP SIGNATURE----- 與 -----END PGP SIGNATURE----- 中間」的那串亂碼了！你只需要使用官方提供的公鑰便可以驗證這一切的資訊是否源自官方。

萬一駭客更改了檔案，則無法通過該文檔的 Hash (雜湊) 驗證，若駭客連該文檔一起修改，將檔案對應的雜湊值也更改了，但由於駭客沒有官方所釋出的公鑰所對應的私鑰，因此也無法對修改後的訊息進行官方簽章。

Hash (雜湊) 其實可以被破解？
#

雜湊也並非無敵，它只是盡量的避免了原文被修改成其他有意義的內容，藉此達到降低被欺騙的可能而已。
有些網站標榜能破解 Hash (雜湊)，那其實是利用大數據來進行比對，尋找雜湊值是否存在於曾經被紀錄的雜湊值與其對應的原文中，「暴力攻擊 (Brute-force attack)(又稱 窮舉攻擊 (Exhaustive attack) 或 爆破)」或者「彩虹表 (Rainbow Table)」。

暴力攻擊 (Brute-force attack)
暴力攻擊其實就是以「窮舉」的方式來找出該雜湊值對應的明文，因此需要嘗試許多種的可能性，也非常耗時，通常不太會真正的窮舉，畢竟可能性太多了。
假設我們是要利用該方法來找出某一串「已知是人工輸入的密碼的雜湊值」的明文，那只要我們可以收集許多常見密碼的列表，就可以使用這些列表來嘗試，萬一該密碼有在列表中，就可以成功找到比對一致的結果。而這種方式依賴的那個裝著許多待比對的字串的檔案我們稱它為「字典檔」。
將字典檔中的各項可能結果使用腳本或特定程式一個個的雜湊後，再去比對是否有與欲破解的雜湊值有相符結果，若沒有則繼續嘗試下一筆資料，若成功批配，則表示該項就是(幾乎是)該雜湊值的原文，同時我們也稱這種雜湊過後得出相同值的狀況為「發生碰撞」。
彩虹表 (Rainbow Table)
嚴格來說也算是一種暴力攻擊的方式，但在某些時候效率比暴力攻擊更高。
通常是指將雜湊的公式逆向運算回推所預先計算好的表。在密碼學打滾的人一定都知道這個！
關於彩虹表的原理解釋相對較複雜，簡單來說就是…
假設原本的雜湊函式為 H，則創建一個與其對應的相反函式 R 又稱「歸約函式 (Reduction function)」。函式 R 可以將利用函式 H 所計算出的雜湊值反算回與原本格式類似的亂碼，這裡也可以理解成是將這雜湊值 Hash 成 新雜湊值，而這個新雜湊值格式是類似原文的格式。就這樣持續的經過 R 運算、H 運算、R 運算、H 運算… 形成了一條很長的鏈，由於這條鏈的結果是必然的，因此只需要對該鏈的初始節點及末端節點儲存即可。
假設原文為「aaaaaa」在經過 H 運算 之後雜湊值為「281DAF40」，則我們將該雜湊值用 R 運算 得出一個反雜湊值為「sgfnyd」之後再進行一次 H 運算 得出「920ECF10」再進行 R 運算 得出「kiebgt」，之後將這條鏈存入表中(只存頭尾節點)。過程如下圖：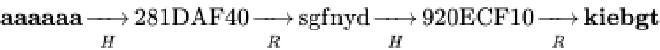
圖源自 Wiki 維基百科

若欲破解的雜湊值所運算出的雜湊鏈中的任意節點與表中的某項末端節點發生碰撞，就可以由該鏈的初始節點開始嘗試重建對應的雜湊鏈。
延續剛剛的情境，假設欲破解的雜湊值為「920ECF10」，在使用 R 運算 後得出「kiebgt」。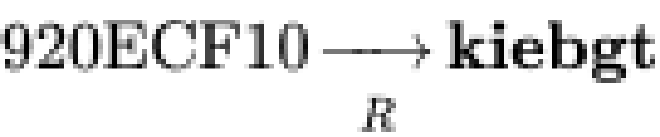
圖源自 Wiki 維基百科

我們發現該值出現在表中，於是我們將該鏈的初始節點開始進行 H 及 R 運算 直到找出「920ECF10」為止，若成功找到，則表示該鏈中的「920ECF10」的前個節點便是解，即為下圖的「sgfnyd」。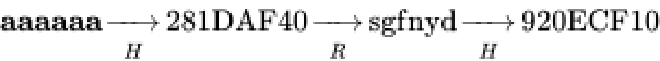
圖源自 Wiki 維基百科

但由於剛剛說過，雜湊是可能會重複的，因此在此情境中，即便「kiebgt」在表中的某項末節點被找到，但也可能發生當你嘗試利用該鏈的初始節點開始進行運算後，也無法找到「920ECF10」的狀況，對此我們稱作「誤報 (False alarm)」，接著只需要跳過該次批配，繼續做運算嘗試找出下個配對即可。
舉例上述情境可能在「FB107E70 (不同的雜湊值)」進行 R 運算 後得出「kiebgt (有著一樣的雜湊)」。
圖源自 Wiki 維基百科