三分之一的機率中,可以透過更換選擇來提高機率,這是曾經讓許多人摸不著頭緒的 Monty-Hall Problem (三門問題),你能參透其中的答案嗎?
起源#
Monty-Hall Problem 又稱三門問題、山羊問題、蒙提霍爾問題。
起源是一個源自Game Theory (博奕論)的數學遊戲問題,最早推測可能出自 1963 年的一個美國電視遊戲節目 - 「Let's Make a Deal (讓我們一起交易)」,其中該節目的主人名為「Monty Hall」,故稱做「Monty-Hall Problem」。
三門遊戲#
在節目中,參賽者的面前會有三道關閉的門,其中一道門後有著一輛汽車,其餘兩道門後則是山羊(我也不知道為啥是山羊…),若是參賽者選中門後為汽車的門,那麼即可贏得汽車。
遊戲開始後,主持人會要求參賽者選擇一道門,不論這道門後是汽車或者山羊,主持人都會開啟參賽者所選的門之外,其餘兩道門中含有山羊的那道門 (主持人是知道門後狀況的)。
舉例,三道門分別為 A、B、C ,參賽者選擇了 C ,若是 B、C 門後皆為山羊,那麼主持人則會開啟 B 門;若是 A、B 門後為山羊,那麼主持人隨機選擇開啟 A 或 B 門。
到目前為止沒什麼太大問題,這時候我們探討的核心問題是…
「在主持人打開一道背後是山羊的門後,會詢問參賽者是否要更換剛剛所選的門,若是選擇換門,那麼參賽者贏得汽車的的機率是否會增加?」
聽起來很荒謬對吧!換不換門,其實對於結果並不會改變才對。
但若是我告訴你,這的確會使得贏得汽車的機率提高至 1/2 呢?
驗證#
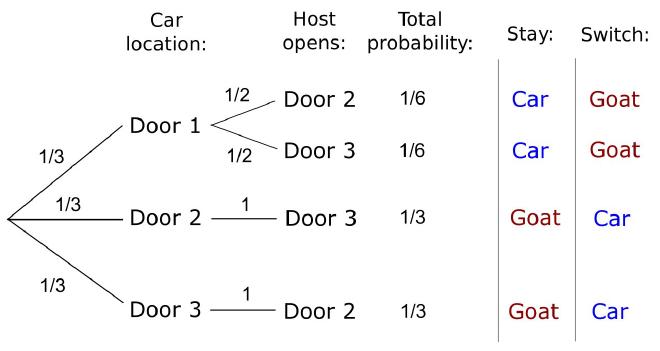
為了方便探討機率,我們實際列舉所有可能性:
先假設
A、B門後是山羊,而C門後則是汽車
- 不換門
- 參賽者堅持選擇
A門,獲得山羊- 參賽者堅持選擇
B門,獲得山羊- 參賽者堅持選擇
C門,獲得汽車由此可知,贏得
汽車機率為1/3
- 換門
- 參賽者選擇
A門,主持人開B門,參賽者換C門,獲得汽車- 參賽者選擇
B門,主持人開A門,參賽者換C門,獲得汽車- 參賽者選擇
C門,主持人開A門,參賽者換B門,獲得山羊- 參賽者選擇
C門,主持人開B門,參賽者換A門,獲得山羊欸?贏得
汽車的機率變成1/2!?
這太不符合常理了,怎麼可能在選擇過後機率發生改變!?
別擔心,帶你繼續看下去。
但在解答之前,喜歡解題的朋友,可以先停在這邊好好思考一下。
解答#
其實,機率是沒有變的,一直都是 1/2!
在一開始的選擇當中,三道門選一道的機率確實是 1/3,但在主持人開啟一道門後(後面是山羊的門),這等於刪除了一道門,此刻若是再給參賽者一次選擇,這次的選擇機率將會是 1/2,重點在於,我們必須將前後兩次選擇視為 獨立事件,真正影響參賽者贏得汽車機率的關鍵在於第二次的選擇。
我們再來重新列舉一次可能性:
先假設
A、B門後是山羊,而C門後則是汽車
並且 主持人已經開啟一道門 (第一次選擇不重要,此指的選擇是第二次選擇)
- 不換門
- 主持人刪除
B門,參賽者仍選擇A門,獲得山羊- 主持人刪除
A門,參賽者仍選擇B門,獲得山羊- 主持人刪除
A門,參賽者仍選擇C門,獲得汽車- 主持人刪除
B門,參賽者仍選擇C門,獲得汽車機率為
1/2
沒錯,這道陷阱題使人容易忽略了參賽者選擇汽車那道門時,主人持人選擇刪除門的可能性是有兩種的。
結論#
這麼一來你知道為什麼了嗎?(如果還是很矇,可以再重頭看一次XD)
有時候看一件事物時, 第一直覺 有可能會是 錯 的,當你深信自己的第一直覺而不求證時,很容易造成如同該題目一般的狀況,一直反覆的問自己為什麼,總是不能理解為什麼機率為 1/2 。
那是因為題目一開始就告訴你機率是 1/3 ,而我們在看到題目是「三道門選一道」的時候,就對此深信不已。